zaman tənliyi

Zaman və ya vaxt — fizikada və başqa təbiət elmlərində bizim kainatın ölçüsü kimi qəbul edilir. O ölçüləbilmə qabiliyyətinə malik olub kainatda baş verən istənilən materiya dəyişiklikləri ilə əlaqədardır. Zaman köklü fenomenlərlə izah oluna bilmədiyindən, o ölçmə yolu ilə qiymətləndirilir. Sİ vahidlər sistemində zaman saniyə (s) ilə ölçülür. Bunun əsasında dəqiqə, saat, gün və həftə əmələ gəlir. Təqvimdən asılı olaraq ay, il, əsr və minilliklər də mövcuddur. Zamanın ölçülməsi astronomiyanın qədim məsələlərindən biridir. Astronomiyada günəş günü və ulduz günü arasında fərq vardır. Bu fərq il boyu bir gün edir. Günəş günü Sİ vahidlər sistemində heç bir vahidə malik deyil.

Davamlılıq tənliyi, axdığı boru içərisindəki duruların (mayelərin) axını, onu qoruyub saxlayan bir tənlikdir. Kütlə, enerji, impuls, elektrik yükü və digər təbii miqdarlar lazımi şəraitdə saxlanıldığı üçün müxtəlif fiziki hadisələri davamlılıq tənliyi ilə təsvir etmək olar. == Sıxılmış durular için davamlılıq tənliyi == ρ 1 ⋅ V 1 ⋅ A 1 = ρ 2 ⋅ V 2 ⋅ A 2 {\displaystyle \rho _{1}\cdot \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\rho _{2}\cdot \mathbf {V} _{2}\cdot \mathbf {A} _{2}} burada; ρ {\displaystyle \rho \,} : Sıxlıq , V {\displaystyle \mathbf {V} } Durunun sürəti , A {\displaystyle \mathbf {A} } : Məhdud (Enkesit) vektorial sahədir . == Sıxılmayan durular için davamlılıq tənliyi == V 1 ⋅ A 1 = V 2 ⋅ A 2 {\displaystyle \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\mathbf {V} _{2}\cdot \mathbf {A} _{2}} burada; V {\displaystyle \mathbf {V} } Durunun sürəti , A {\displaystyle \mathbf {A} } : Məhdud (Enkesit) vektorial sahədir .

Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir. == Xətti Diofant tənlikləri == Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər; Nümunə 1.1 x + y = 1 {\displaystyle x+y=1} Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. ( y = 1 − x {\displaystyle y=1-x} ). Bu bərabərliyin həll çoxluğu; (X, 1 − X) şəklindədir hər X ∈ Z üçün Nümunə 1.2 x + 2 y = 1 {\displaystyle x+2y=1} Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür ( x = 1 − 2 y {\displaystyle x=1-2y} ). Bu bərabərliyin həll çoxluğu; (1-2y, y) şəklindədir hər y ∈ Z üçün Nümunə 1.3 3 x + 6 y = 1 {\displaystyle 3x+6y=1} Bu bərabərliyin həlli boş çoxluqdur. Hər x {\displaystyle x} və y {\displaystyle y} tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz. === Ümumi xətti Diofant tənliyi === a x + b y = c {\displaystyle ax+by=c} şəklindədir. Burada a, b və c tam əmsallar x {\displaystyle x} və y {\displaystyle y} tam ədəd dəyişənləridir. == Digər nümunələr == === Pifaqor teoremi === Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi) Nümunə 2.1.1 x 2 + y 2 = z 2 {\displaystyle x^{2}+y^{2}=z^{2}\,} Burada x , y , z {\displaystyle x,y,z} tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir. == Xətti Diofant tənlikləri == Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər; Nümunə 1.1 x + y = 1 {\displaystyle x+y=1} Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. ( y = 1 − x {\displaystyle y=1-x} ). Bu bərabərliyin həll çoxluğu; (X, 1 − X) şəklindədir hər X ∈ Z üçün Nümunə 1.2 x + 2 y = 1 {\displaystyle x+2y=1} Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür ( x = 1 − 2 y {\displaystyle x=1-2y} ). Bu bərabərliyin həll çoxluğu; (1-2y, y) şəklindədir hər y ∈ Z üçün Nümunə 1.3 3 x + 6 y = 1 {\displaystyle 3x+6y=1} Bu bərabərliyin həlli boş çoxluqdur. Hər x {\displaystyle x} və y {\displaystyle y} tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz. === Ümumi xətti Diofant tənliyi === a x + b y = c {\displaystyle ax+by=c} şəklindədir. Burada a, b və c tam əmsallar x {\displaystyle x} və y {\displaystyle y} tam ədəd dəyişənləridir. == Digər nümunələr == === Pifaqor teoremi === Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi) Nümunə 2.1.1 x 2 + y 2 = z 2 {\displaystyle x^{2}+y^{2}=z^{2}\,} Burada x , y , z {\displaystyle x,y,z} tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Dreyk tənliyi — qalaktikada bizimlə əlaqəyə girmək ehtimalı olan sivilizasiyaların sayını hesablamağa imkan verən riyazi formul. Formul aşağıdakı kimidir: N = R ⋅ f p ⋅ n e ⋅ f l ⋅ f i ⋅ f c ⋅ L {\displaystyle N=R\cdot f_{p}\cdot n_{e}\cdot f_{l}\cdot f_{i}\cdot f_{c}\cdot L} burada, N {\displaystyle ~N} — əlaqəyə girməyə hazır olan sivilizasiyaların sayı; R {\displaystyle ~R} — il ərzində bizim qalaktikada yaranan ulduzların sayı; f p {\displaystyle ~f_{p}} — planetləri olan ulduzların xüsusi çəkisi; n e {\displaystyle ~n_{e}} — sivilizasiyanın yaranması üçün müvafiq şəraitə malik olan planetlərin və peyklərin sayı; f l {\displaystyle ~f_{l}} — müvafiq şəraitə malik olan planetdə həyatın yaranması ehtimalı; f i {\displaystyle ~f_{i}} — həyat olan planetdə şüurlu varlıqların yaranma ehtimalı; f c {\displaystyle ~f_{c}} — əlaqəyə hazır olan və əlaqəyə girmək istəyən şüurlu sakinlərə malik planetlərlə, şüurlu sakinləri olan planetlərin sayına nisbəti; L {\displaystyle ~L} — bu sivilizasiyaların ömür müddəti. Formul Kaliforniyanın Santa-Kruz Universitetinin astronomiya və astrofizika professoru Frenk Donald Dreyk tərəfindən 1960-cı ildə təklif olunmuşdur. Onun 1961-ci ildə ehtimal olunan rəqəmlər əsasında apardığı hesablama aşağıdakı kimi olmuşdur. R = 10/il (ildə 10 ulduz yaranır) fp = 0.5 (ulduzların yarısının planetləri var) ne = 2 (sitemdə orta hesabla 2 planet həyat üçün yararlıdır) fl = 1 (əgər həyatın yaranma ehtimalı varsa, o mütləq yaranır) fi = 0.01 (həyatın şüurlu formayadək inkişaf etməsi ehtimalı – 1 %) fc = 0.01 (sivilizasiyaların 1 %-i əlaqə yaratmaq imkanına malik olacaq və əlaqə qurmaq istəyəcək) L = 10 000 il (texniki cəhətdən inkişaf etmiş sivilizasiya 10000 il mövcud olur) Bu təxmini hesablamaya əsasən N = 10 × 0,5 × 2 × 1 × 0,01 × 0,01 × 10000 = 10. Tənlikdəki göstəricilərdən yalnız R {\displaystyle ~R} və f p {\displaystyle ~f_{p}} astronomiyanın indiki inkişaf səviyyəsində müəyyən qədər dəqiq müəyyənləşdirilə bilər. Digər göstəricilərin müəyyənləşdirilməsi mümkün olmadığından Dreyk tənliyi kəskin tənqidlərlə qarşılaşmışdır.

Koşi ötürmə tənliyi Optikada müəyyən bir şəffaf material üçün işığın sınma indeksi və dalğa uzunluğu arasında empirik əlaqə . Adını 1837-ci ildə təyin edən riyaziyyatçı Oqüsten Koşinin şərəfinə almışdır. == Tənlik == Koşi tənliyinin ən ümumi forması n ( λ ) = A + B λ 2 + C λ 4 + ⋯ , {\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}}+{\frac {C}{\lambda ^{4}}}+\cdots ,} burada n sınma əmsalıdır, λ dalğa uzunluğu, A, B, C və s., tənliyi məlum dalğa uzunluqlarında ölçülmüş sındırma göstəricilərinə uyğunlaşdırmaqla material üçün müəyyən edilə bilən əmsallardır . Əmsallar adətən mikrometrlərdə vakuum dalğa uzunluğu (materialın daxilində olan λ/n kimi deyil) kimi λ üçün göstərilir. Adətən, tənliyin ilk iki həddindən istifadə etmək kifayətdir: n ( λ ) = A + B λ 2 , {\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}},} burada A və B əmsalları tənliyin bu forması üçün xüsusi olaraq təyin edilir. Ümumi optik materiallar üçün əmsallar cədvəli aşağıda göstərilmişdir: işıq-maddə qarşılıqlı əlaqəni əsaslandıran Koşinin bu tənliyi sonradan yanlış olduğu məlum oldu. Xüsusilə, tənlik yalnız görünən dalğa uzunluğu bölgəsində normal dispersiya bölgələri üçün keçərlidir. İnfraqırmızı dalğalarda tənlik qeyri-dəqiq olur və anomal dispersiya bölgələrini təmsil edə bilmir. Buna baxmayaraq, onun riyazi sadəliyi onu bəzi tətbiqlərdə faydalı edir. Zelmeyer tənliyi anomal dispersiv bölgələri əhatə edən və ultrabənövşəyi, görünən(400-700 nm dalğa uzunluqlu şüalar) və infraqırmızı spektrdə materialın sındırma indeksini daha dəqiq modelləşdirən Koşinin çalışmasının genişləndirilmiş formasıdır.

Laplas tənliyi riyaziyyatda və fizikada ikitərtibli xüsusi törəməli diferensial tənlikdir. Xüsusiyyətləri ilk dəfə Pyer Simon Laplas tərəfindən tətqiq edildiyinə görə onun adını daşıyır. Tənliyin yazılışı aşağıdaki kimidir: ∇ 2 f = 0 və ya Δ f = 0 , {\displaystyle \nabla ^{2}\!f=0\qquad {\mbox{və ya}}\qquad \Delta f=0,} Burada Δ = ∇ ⋅ ∇ = ∇ 2 {\displaystyle \Delta =\nabla \cdot \nabla =\nabla ^{2}} Laplas operatoru, ∇ ⋅ {\displaystyle \nabla \cdot } divergensiya operatoru, ∇ {\displaystyle \nabla } qradiyent operatoru və f ( x , y , z ) {\displaystyle f(x,y,z)} isə iki dəfə diferensiallana bilən həqiqi qiymətli funksiyadır. Belə ki, Laplas operatoru skalyar bir funksiyanı başqa skalyar funksiyaya inkas etdirir. Sağ tərəfdə h ( x , y , z ) {\displaystyle h(x,y,z)} funksiyası təyin olunarsa, onda Laplas tənliyi aşağıdaki kimi verilir: Δ f = h . {\displaystyle \Delta f=h.} Buna Puasson tənliyi, Laplas tənliyinin ümumiləşdirilməsi deyilir. Laplas və Poisson tənlikləri eliptik xüsusi törəməli diferensial tənliklərin ən sadə nümunələridir. Laplas tənliyi, həmçiin Helmholtz tənliyinin xüsusi bir haldır. Laplas tənliyinin həllərinin ümumi nəzəriyyəsi potensial nəzəriyyə olaraq bilinir. Laplas tənliyinin həlli fizikanın bir çox sahələrində, xüsusən elektrostatikada, qravitasiya və maye dinamikasında mühüm əhəmiyyət daşıyan harmonik funksiyalardır.

y ′ + a ( x ) y + b ( x ) y 2 + c ( x ) = 0 {\displaystyle y^{\prime }+a(x)y+b(x)y^{2}+c(x)=0} ( ∗ ) {\displaystyle (*)} şəklində tənliyə Rikkati tənliyi deyilir. Rikkati tənliyi b ( x ) = 0 {\displaystyle b(x)=0} olduqda xətti, c ( x ) = 0 {\displaystyle c(x)=0} olduqda isə Bernulli tənliyinə çevrilir. Rikkati tənliyinin hər hansı y 1 ( x ) {\displaystyle y_{1}(x)} xüsusi həlli məlum olduqda y ( x ) = y 1 ( x ) + z ( x ) {\displaystyle y(x)=y_{1}(x)+z(x)} əvəzləməsi vasitəsilə Bernulli tənliyinə gətirlir. Ümumi halda, Rikkati tənliyi kvadraturaya gətirilə bilmir, yəni həll etmək olmur. Xüsusi halda: b d x d t = x 2 + a t α , ( ∗ ∗ ) {\displaystyle b{\frac {dx}{dt}}=x^{2}+at^{\alpha },\quad (**)} haradakı α , a , b ≠ 0 {\displaystyle \alpha ,\,a,\,b\neq 0} —sabiti, ilk dəfə italyan riyaziyyatçısı tədqiq etmişdir Yakopo Françesko Rikkati və ailələrini Bernulli . α = 4 n / ( 1 − 2 n ) , n ∈ N , {\displaystyle \alpha ={4n}/{(1-2n)},\ n\in \mathbb {N} ,} или α = − 2 {\displaystyle \alpha =-2} Jozef Liuvill (1841)isbat etmişdir. ( ∗ ) {\displaystyle (*)} şəkildə ümumi Rikkati tənliyi , ( ∗ ∗ ) {\displaystyle (**)} — isə xüsusi Rikkati tənliyi adlanır. y ′ + m ( x ) ( A y + B y 2 + C ) = 0 {\displaystyle y^{\prime }+m(x)(Ay+By^{2}+C)=0} olduqda dəyişənlərinə ayrılan, y ′ + A y x + B ( y x ) 2 + C = 0 {\displaystyle y^{\prime }+A{\frac {y}{x}}+B\left({\frac {y}{x}}\right)^{2}+C=0} olduqda bircins, y ′ + A y x + B ( y ) 2 + C x 2 = 0 {\displaystyle y^{\prime }+A{\frac {y}{x}}+B(y)^{2}+{\frac {C}{x^{2}}}=0} olduqda ümumiləşmiş bircns tənliyə çevrilir. y ′ + 2 y e x − y 2 = e 2 x + e x {\displaystyle y^{\prime }+2ye^{x}-y^{2}=e^{2x}+e^{x}} Rikkati tənliyini həll edin. y 1 ( x ) = e x {\displaystyle y_{1}(x)=e^{x}} tənliyin həlli olduğunu bilavasitə yoxlamaq olar.

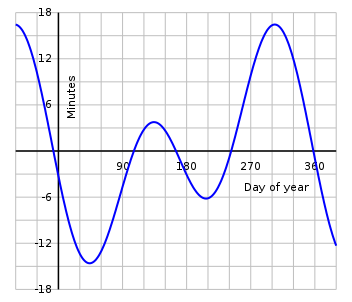
Vaxt tənliyi — eyni an üçün verilmiş coğrafi meridianda orta və həqiqi Günəş vaxtlarının fərqidir. η = T m − T ⊙ = t m − t ⊙ {\displaystyle \eta =T_{m}-T_{\odot }=t_{m}-t_{\odot }} Vaxt tənliyini əslində vaxt düzəlişi adlandırmaq daha doğru olardı, lakin o tarixi olaraq astronomiyaya vaxt tənliyi kimi daxil olmuşdur.

Vəziyyət tənliyi - termodinamikanın makroskopik sistemlərini (temperatur, təzyiq, həcm, kimyəvi potensial və s.) bir-biri ilə əlaqələndirən tənlikdir. f ( P , V , T ) = 0. {\displaystyle f(P,\;V,\;T)=0.} U = U ( T , V ) , {\displaystyle U=U(T,V),} U = U ( T , P ) , {\displaystyle U=U(T,P),} U = U ( V , P ) . {\displaystyle U=U(V,P).} U = U ( S , V ) {\displaystyle U=U(S,\;V)} (daxili enerji üçün kanonik vəziyyət tənliyidir), H = H ( S , P ) {\displaystyle H=H(S,\;P)} (entalpiya üçün kanonik vəziyyət tənliyidir), F = F ( T , V ) {\displaystyle F=F(T,\;V)} (Helmhots enerjisi üçün kanonik vəziyyət tənliyidir), G = G ( T , P ) {\displaystyle G=G(T,\;P)} (Qibbs potensialı üçün kanonik vəziyyət tənliyidir). Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6. Van der Waals, J. D. (1873). On the Continuity of the Gaseous and Liquid States (doctoral dissertation).

Zelmeyer tənliyi müəyyən bir şəffaf mühit üçün sınma indeksi və dalğa uzunluğu arasında empirik əlaqədir . Tənlik işığın mühitdə dispersiyasını təyin etmək üçün istifadə olunur. İlk dəfə 1872-ci ildə Volfqanq Zelmeyer tərəfindən təklif edildi və Augustin Cauchy -nin dispersiyanın modelləşdirilməsi üçün kəşf etdiyi Koşi tənliyinin ümumiləşdirilmiş forması idi. Orijinal və ən ümumi formada Zelmeyer tənliyi aşağıdakı kimi verilir n 2 ( λ ) = 1 + ∑ i B i λ 2 λ 2 − C i {\displaystyle n^{2}(\lambda )=1+\sum _{i}{\frac {B_{i}\lambda ^{2}}{\lambda ^{2}-C_{i}}}} , burada n sınma əmsalı, λ dalğa uzunluğu, Bi və Ci isə eksperimental olaraq müəyyən edilmiş Zelmeyer əmsallarıdır . Bu əmsallar adətən mikrometrlərdə λ üçün göstərilir. Qeyd edək ki, bu λ vakuum dalğa uzunluğudur, yəni materialın daxilində olan λ/n formasında deyil. Tənliyin fərqli forması bəzən müəyyən növ materiallar üçün istifadə olunur, məsələn, kristallar. Cəmin hər həddi, C i {\displaystyle {\sqrt {C_{i}}}} dalğa uzunluğunda Bi -in absorbsiya rezonansını təmsil edir. Məsələn, BK7 şüşəsi üçün aşağıdakı əmsallar ultrabənövşəyi şüada iki, orta infraqırmızı bölgədə isə bir udma rezonansına uyğun gəlir. Hər bir absorbsiya zirvəsinin yaxınında tənlik n2 = ±∞ qeyri-fiziki qiymətləri verir və bu dalğa uzunluğu bölgələrində Helmholtzun tənliyi kimi daha dəqiq dispersiya modelindən istifadə edilməlidir.

Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır. Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır. Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.

Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır. Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır. Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.

Məkan-zaman və ya fəza-zaman anlayışı – nisbilik nəzəriyyəsində məkan və zamanın vahid 4 ölçülü koordinat sisteminin müxtəlif hissələri kimi götürülməsindən formalaşıb. Nisbilik nəzəriyyəsi kəşf olunana qədər mexanikada Nyuton qanunları və Qalileyin nisbilik prinsipi əsas yeri tuturdu. Bu çərçivədə məkan, sərbəst hərəkətin mümkün olduğu və 3 ölçülü koordinat sistemi ilə təsvir oluna biləcək mühit, zaman isə bu fəzadakı hərəkəti xarakterizə edən kəmiyyət olaraq götürülürdü. Beləliklə, nisbilik nəzəriyyəsindən əvvəl məkan və zaman bir-birindən ayrı anlayışlar idi. Lakin Albert Eynşteyn zaman və uzunluğun nisbi anlayışlar olduğunu göstərdikdən sonra alman riyaziyyatçısı Herman Minkovski, hadisələri 3 ölçülü fəzada dəyərləndirmək əvəzinə 4 ölçülü fəzazaman koordinat sistemində dəyərləndirməyin daha əlverişli olduğu qənaətinə gəldi. Belə olduqda zaman özü keçmişdən gələcəyə doğru bir istiqamət kimi götürülürdü. Ümumi nisbilik nəzəriyyəsinin kəşf olunmasında xüsusi nisbilik nəzəriyyəsinin, Minkovski koordinat sistemində təsviri böyük rol oynayıb.

Məhəmməd Zaman və ya Məhəmməd Paolo Zaman Kermani (d. 1680-ci ildən əvvəl – ö. 1700-cü ildən sonra) — Səfəvi imperiyasında fəaliyyət göstərən məşhur rəssam və xəttat. Səfəvi imperiyası miniatür sənətində XVII əsrin ortalarında yaranmağa başlayan Farangi-Sazi üslubunun ən görkəmli nümayəndələrindən biri hesab edilir. Təxminən 1680-ci ildə dünyaya gəlmiş, fəaliyyəti nəticəsində məşhur Səfəvi xəttatlarından və rəssamlarından birinə çevrilmişdir. Əslən Kermandan olsa da, Təbrizdə təhsil almışdır. II Şah Abbasın hakimiyyəti dövründə şah tərəfindən rəssamlıq sənəti alması üçün Romaya göndərilmişdir, lakin buradakı təhsili zamanı Katolik olmuş və Paolo adını qəbul etmişdir. Din dəyişdirdiyinə görə, Səfəvi imperiyasına geri döndükdən sonra problem yaşamışdır. Xristianlığı qəbul etməsinin aşkarlanmasından sonra Böyük Moğol imperiyasına qaçmış, moğol sülaləsi tərəfindən qəbul edilərək saraya yerləşdirilmişdir. O, rəssam və xəttat kimi italyan rəssamların texnikasından təsirlənmişdir.

Zaman — Azərbaycanda kişi adı. Zaman Abdulla — Azərbaycanlı şair. Zaman Əsgərli — Azərbaycan ədəbiyyatşünası, tənqidçi, publisist.

Zaman — ölçülə bilən fiziki kəmiyyət. Həmçinin aşağıdakı mənalara da gələ bilər; Zaman — hadisələrin müəyyən ardıcıl gedişinin dərki; Zaman — Türkiyədə nəşr olunan gündəlik qəzet Zaman — qrammatikada hadisələrin gedişini təsvir edən forma.

Zaman və ya vaxt — fizikada və başqa təbiət elmlərində bizim kainatın ölçüsü kimi qəbul edilir. O ölçüləbilmə qabiliyyətinə malik olub kainatda baş verən istənilən materiya dəyişiklikləri ilə əlaqədardır. Zaman köklü fenomenlərlə izah oluna bilmədiyindən, o ölçmə yolu ilə qiymətləndirilir. Sİ vahidlər sistemində zaman saniyə (s) ilə ölçülür. Bunun əsasında dəqiqə, saat, gün və həftə əmələ gəlir. Təqvimdən asılı olaraq ay, il, əsr və minilliklər də mövcuddur. Zamanın ölçülməsi astronomiyanın qədim məsələlərindən biridir. Astronomiyada günəş günü və ulduz günü arasında fərq vardır. Bu fərq il boyu bir gün edir. Günəş günü Sİ vahidlər sistemində heç bir vahidə malik deyil.

Zaman fəlsəfədə baş verən hadisələrin ardıcıllığının insan tərəfindən dərk edilməsidir. Bu dəyişikliklər "zamanın istiqamətini" əsaslandırırlar. Zamanın mövcudluğunu Platon, Aristotel, Avqust, Leybnits, Kant kimi dahi filosoflar müxtəlif şəkildə təsvir etmişlər. Gündəlik həyatdan məlumdur ki, zaman dərk oluna bilməyən obyektlərdən asılı olmayaraq da mövcuddur. Buna görə də, zamanın təsvirində həmişə belə bir sual ortaya çıxırdı ki, zaman insanların düşüncəsində xüsusi baxış formalaşdıqdan sonra mövcud olmuş, ya da ondan asılı olmayaraq obyektiv, bərabərformalı və mütləq mövcuddur. Bu sualın cavabı əsrlər boyu fəlsəfənin, teologiyanın və mistikanın əsas mövzusu olmuşdur. Son zamanlarda fizika, astronomiya, neurologiya, xronopsixologiya və başqa elm sahələri də zamanın tədqiqində öz töhfələrini vermişlər. Zamanın mövcudluğu öz-özlüyündə problem yaradır, çünki, mövcudluq anlayışının vaxtla əlaqələndirilməsi çətindir. İnsan beynində aparılan son tədqiqatlar, molekulyar biologiya və psixologiya göstərmişdir ki, insanda dərketmə, düşünmə, yadasalma, vaxt hissi və şüur bir-biri ilə o dərəcədə sıx bağlıdır ki, onlar adi halda bir-birindən ayrıla bilməzlər. Zaman, düşüncə və insan şüuru birlikdə fəaliyyət göstərirlər.

İndiki zaman — cari anda baş verən hadisələrdən, yəni məkan-zamanın müəyyən bir sahəsindən ibarət olmaqla zaman oxunun bir hissəsidir. Müəyyən fərziyyələrə görə, indiki vaxt cari günlərə, aylara və hətta illərə də aiddir. Bu mənada indiki zaman keçmişə (artıq baş vermiş bir çox hadisələr) və gələcəyə (hələ baş verməmiş bir çox hadisələr) qarşı durur və onların arasında yerləşir.

Məkan-zaman və ya fəza-zaman anlayışı – nisbilik nəzəriyyəsində məkan və zamanın vahid 4 ölçülü koordinat sisteminin müxtəlif hissələri kimi götürülməsindən formalaşıb. Nisbilik nəzəriyyəsi kəşf olunana qədər mexanikada Nyuton qanunları və Qalileyin nisbilik prinsipi əsas yeri tuturdu. Bu çərçivədə məkan, sərbəst hərəkətin mümkün olduğu və 3 ölçülü koordinat sistemi ilə təsvir oluna biləcək mühit, zaman isə bu fəzadakı hərəkəti xarakterizə edən kəmiyyət olaraq götürülürdü. Beləliklə, nisbilik nəzəriyyəsindən əvvəl məkan və zaman bir-birindən ayrı anlayışlar idi. Lakin Albert Eynşteyn zaman və uzunluğun nisbi anlayışlar olduğunu göstərdikdən sonra alman riyaziyyatçısı Herman Minkovski, hadisələri 3 ölçülü fəzada dəyərləndirmək əvəzinə 4 ölçülü fəzazaman koordinat sistemində dəyərləndirməyin daha əlverişli olduğu qənaətinə gəldi. Belə olduqda zaman özü keçmişdən gələcəyə doğru bir istiqamət kimi götürülürdü. Ümumi nisbilik nəzəriyyəsinin kəşf olunmasında xüsusi nisbilik nəzəriyyəsinin, Minkovski koordinat sistemində təsviri böyük rol oynayıb.

Zaman Arzuman oğlu Mirzəzadə (8 fevral 1995, Lənkəran) — müdafiə mövqeyində çıxış edən Azərbaycan futbolçusu, mövqe müdafiəçisi. Mirzəzadə uşaq yaşlarından "Xəzər Lənkəran" FK-da çıxış etmişdir. O, 2015-ci ildə əsas komandaya keçmiş, klub ləğv olunana qədər klubda çıxış etmişdir. Zaman Arzuman oğlu Mirzəzadə 8 fevral 1995-ci ildə Azərbaycanın Lənkəran şəhərində anadan olmuşdur. Zaman Mirzəzadə "Xəzər Lənkəran" FK-nın yetirməsidir. O, 12 yaşında uşaq yaş kateqoriyasında karyerasına başlamışdır. Mirzəzadə "Xəzər Lənkəran"ın 17 yaşadək komandasında çıxış etmiş, 2012-ci ildə klubun gənclər komandasına keçid etmişdir. O, 2014-cü ildən əsas komandada çıxış etməyə başlamışdır. Bundan başqa, Mirzəzadə həm də ehtiyat komanda üçün çıxış etmişdir. O, Topaz Premyer Liqasının 2014/2015 mövsümündə, 2 may 2015-ci il tarixində klubun əsas heyətində eyni liqada çıxış edən "Bakı" FK ilə səfər oyununda debüt etmişdir.

Zaman-Azərbaycan - "Zaman-Azər MMC"-nin təsis etdiyi qəzetdir. "Zaman-Azərbaycan" qəzeti ilk dəfə 1991-ci ilin may ayının 24-də çap olunmuşdur. "Zaman-Azərbaycan"ın ilk nəşrləri İstanbulda çap olunaraq, təyyarə ilə Bakıya gətirilmişdir. O zamanlar Azərbaycan hələ müstəqilliyini bərpa etməmişdi. Sovet İttifaqı dağıldıqdan sonra, Azərbaycan müstəqilliyini elan edən kimi "Zaman-Azərbaycan" qəzeti ölkədə ilk xarici qurum kimi qeydiyyatdan keçmişdir. Bundan sonra "Zaman-Azərbaycan" tamamilə Azərbaycanda hazırlanmış və Azərbaycan Dövlət Nəşriyyatında çap olunmuşdur. Müstəqilliyin ilk illərində yalnız köhnə mətbəələr var idi. Ona görə də, rəngli kağız və dünya standartlarına uyğun çap imkanı yox idi. Bu problemi həll etmək üçün "Zaman-Azərbaycan" ilk dəfə ölkəyə rəngli mətbəə gətirmişdir. Bu, Azərbaycan tarixi üçün ilk rəngli mətbəə idi.

Zaman polisi (ing. Timecop) — 1994-cü ildə Piter Hayams tərəfindən çəkilən filmdir. Bu film ABŞ-nin "Dark Horse Comics" nəşriyyatı tərəfindən istehsal edilən, Mark Veraydenin eyniadlı komiksı əsasında filmdir. Zaman polisi — Internet Movie Database saytında.

Zaman cinayətləri (isp. Los cronocrímenes) — Naço Viqalondonun öz yazdığı ssenari əsasında çəkdiyi ispan elmi fantastika filmidir. Rejissor filmdəki rollardan birində də çəkilmişdir. Filmin baş qəhrəmanı üç dəfə eyni günü yaşayır və özünü düşdüyü zaman dövriyyəsindən xilas etməyə çalışır.